Lab4
Oppgaver
Oppvarming
Obligatorisk
Valgfri
Hvordan fullføre laben
For å bestå laben, må alle de obligatoriske oppgavene være bestått. Laben leveres i CodeGrade; du finner som vanlig knappen dit på mitt.uib.
Oppvarming
Fjerne 3-ere
I en fil threes_removed.py, Skriv en (ikke-destruktiv) funksjon threes_removed som tar inn en liste med tall a som parameter. Funksjonen skal returnere en ny liste med tall slik at alle forekomster av tallet 3 blir borte. Rekkefølgen skal være lik som i den originale listen a.
Test koden din ved å legge til disse linjene nederst i filen:
print('Tester threes_removed... ', end='')
# Test 1
a = [1, 2, 3, 4]
actual = threes_removed(a)
expected = [1, 2, 4]
assert expected == actual # Sjekker at returverdien er som ønsket
assert [1, 2, 3, 4] == a # Sjekker at input (a) ikke har blitt mutert
# Test 2
a = [1, 2, 3, 3]
actual = threes_removed(a)
expected = [1, 2]
assert expected == actual
assert [1, 2, 3, 3] == a
# Test 3
a = [3, 3, 1, 3, 2, 4, 3, 3, 3]
actual = threes_removed(a)
expected = [1, 2, 4]
assert expected == actual
assert [3, 3, 1, 3, 2, 4, 3, 3, 3] == a
# Test 4
a = [3, 3]
actual = threes_removed(a)
expected = []
assert expected == actual
assert [3, 3] == a
print('OK')
Du kan ta utgangspunkt i denne koden:
def threes_removed(a):
... # Din kode her
# Opprett en tom liste r.
# For hvert element x i a:
# Hvis x ikke er lik 3, legg x til i listen r.
# Returner listen r.
Trollmannens lærling
Du er lærling av den mystiske trollmannen Gallius, som eier en rekke magiske gjenstander. Han har gitt deg som en øvelse å duplisere alle disse gjenstandene med magien din. Dessverre behøver du også å registrere denne endringen i listen som Gallius har over gjenstandene sine og hvor mange han har av hver.
I en fil duplicated.py, lag en ikke-destruktiv funksjon duplicated som tar inn en liste items og returnerer en ny liste hvor hvert element er dobbelt så stort som elementet i den originale listen.
For eksempel, hvis items er [1, 2, 3, 4, 5], skal funksjonen returnere [2, 4, 6, 8, 10].
Du kan kopiere følgende kode inn nederst i duplicated.py for å teste funksjonen din:
print("Testing duplicate... ", end="")
# Første test
a = [1, 2, 3, 4, 5]
actual = duplicated(a)
expected = [2, 4, 6, 8, 10]
assert expected == actual # Sjekker at returverdien er som ønsket
assert [1, 2, 3, 4, 5] == a # Sjekker at input (a) ikke har blitt mutert
# Flere tester
assert [4, 8, 12, 16, 20] == duplicated([2, 4, 6, 8, 10])
assert [0, 0, 0, 0, 0] == duplicated([0, 0, 0, 0, 0])
assert [-2, 4, 2, 10, 100] == duplicated([-1, 2, 1, 5, 50])
print("OK")
- Opprett en ny liste (som du til slutt skal returnere, men som i utgangspunktet er tom).
- Bruk en for-løkke for å gå gjennom verdiene i listen vi blir gitt som input.
- Inne i for-løkken, bruk
.appendfor å legge til det dobbelte av verdien vi ser på til den nye listen. - Returner svaret
Botanist
Du er en botaniker som har vært på en ekspedisjon til en øy som er kjent for sine mange forskjellige planter. Du har samlet inn en rekke planter og har lagret dem i en liste plants. Du har også en liste dangerous_plants som inneholder navnene på alle de farlige plantene på øya. Du trenger å finne ut hvilke av plantene du har samlet inn som er farlige, slik at du kan fjærne dem fra samlingen din.
I en fil botanist.py, lag en funksjon filter_dangerous som tar inn en liste av planter plants og en liste av farlige planter dangerous_plants. Funksjonen skal returnere en liste med plantene i plants som ikke er farlige.
For eksempel, hvis plants er ["rose", "daisy", "lily", "tulip", "dandelion"] og dangerous_plants er ["dandelion", "poison ivy"], skal funksjonen returnere ["rose", "daisy", "lily", "tulip"].
Du kan starte fra denne koden:
def filter_dangerous(plants, dangerous_plants):
# Din kode her
For å løse denne oppgaven, kan du bruke en for-løkke for å iterere over alle plantene i plants. Først lager du en tom liste, kall den gjerne safe_plants. For hver plante i plants, sjekk om den er i dangerous_plants. Hvis den ikke er det, legg den til i safe_plants. Til slutt, returner safe_plants.
Her er kode du kan lime inn på slutten av filen som tester funksjonen:
print("Testing filter_dangerous... ", end="")
assert ["rose", "daisy", "lily", "tulip"] == filter_dangerous(["rose", "daisy", "lily", "tulip", "dandelion"], ["dandelion", "poison ivy"])
assert ["minalia", "cherluvia", "kirina", "ajisai"] == filter_dangerous(["minalia", "cherluvia", "kirina", "ajisai", "evil_plant", "raa"], ["evil_plant", "raa"])
assert ["pythonium"] == filter_dangerous(["pythonium", "haskelia", "shakersperia"], ["haskelia", "jaskria", "shakersperia"])
print("OK")
Pythonesia
Om du ikke allerede kan indeksering av 2d-lister veldig godt, anbefaler vi at du benytter fremgangsmåten og pseudokoden under for å se hvordan du kan iterere over en 2d-liste.
Du er med i en ekspedisjon til Pythonesia, et land som er kjent for sine mange rutenett av tall. Noe du har lest i reisehåndboken er at det er en gammel legende om at det finnes skatter gjemt under et av rutenettene i Pythonesia. Det er nemlig gjemt en skatt under alle ruter hvor radnummeret, kolonnenummeret og verdien i ruten (rad, kolonne) summerer til et spesielt tall. Du tenker du kan bruke dine programmeringsferdigheter til å finne posisjonene til disse skattene.
I en fil find_treasure.py, lag en funksjon find_treasure som tar inn en 2D-liste grid og et tall target_sum. Funksjonen skal returnere en liste av koordinater [row,col] i rutenettet hvor summen av rad, kolonne og verdi er lik target_sum. Hvis det ikke finnes noen slike skatter, skal funksjonen returnere en tom liste.
For eksempel, hvis du har følgende rutenett:
[
[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
]
og target_sum er 5, så skal funksjonen returnere [[0, 2], [1, 0]] siden på rad 0, kolonne 2, så er summen 0 + 2 + 3 = 5, og på rad 1, kolonne 0, så er summen 1 + 0 + 4 = 5. Se bilder under for visualisering:


For å holde styr på indeksene til posisjonene mens vi itererer over de skal vi bruke en nøstet for ... in range(...) type løkke. Dette gjør at vi kan holde styr på indeksene mens vi itererer.
I funksjonen find_treasure gjør følgende:
- Opprett en tom liste
treasuressom skal inneholde koordinatene til skattene. - Definer variabler
rowsogcolssom er henholdsvis antall rader og kolonner i rutenettet. Dette kan du finne ved å brukelenfunksjonen medgridoggrid[0]som argument hver for seg. Mengden sublister i rutenettet (len(grid)) er antall rader, og lengden av en subliste (len(grid[0])) er antall kolonner. Vi velger subliste 0 fordi vi antar at alle sublister har samme lengde. - Lag en ytre løkke
for row in range(rows)og en indre løkkefor col in range(cols). Dette vil la deg iterere over alle mulige kombinasjoner av rad og kolonne. Løkken itererer over hver rad-indeks, og for hver rad itererer den over hver kolonne-indeks. - Inne i den indre løkken: hent ut verdien på posisjonen (row, col)
value = grid[row][col], og sjekk om summen av rad, kolonne og verdi er liktarget_sum. Hvis det er tilfellet, legg koordinatene[row, col]tiltreasures. - Etter at du har gått gjennom alle elementene i rutenettet, returner
treasuressom nå inneholder koordinatene til skattene.
def find_treasure(grid, target_sum):
... # Din kode her
# opprett en tom liste `treasures` som skal inneholde koordinatene til skattene.
# definer en variabel `rows` som er antall rader i rutenettet
# definer en variabel `cols` som er antall kolonner i rutenettet
# lag en ytre løkke `for row in range(rows)`
# lag en indre løkke `for col in range(cols)`
# hent ut verdi til denne posisjonen
# sjekk om summen av radnummer, kolonnenummer og verdi er lik `target_sum`
# hvis det er tilfellet, legg koordinatene ``[row, col]`` til `treasures`
# returner `treasures`
Her er kode du kan sette inn på slutten av find_treasure.py for å teste funksjonen din:
print("Testing find_treasure... ", end="")
# Test 1
grid = [
[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
]
target_value = 5
actual = find_treasure(grid, target_value)
expected = [[0, 2], [1, 0]]
assert expected == actual
# Test 2
actual = find_treasure([[1, 2], [3, 4]], 3)
expected = [[0, 1]]
assert expected == actual
# Test 3
actual = find_treasure([[1, 2], [3, 4]], 1)
expected = [[0, 0]]
assert expected == actual
# Test 4
actual = find_treasure([[1, 2], [3, 4]], 1000)
expected = []
assert expected == actual
print("OK")
Obligatorisk
Gressklipper
Du jobber som gressklipper og har fått i oppgave å klippe gresset i en hage. Eieren av hagen er veldig interessert i å vite den nøyaktige høyden på gresset etter at det er klippet. Du har fått en liste heights som eieren har laget over høyden på gresset på forskjellige steder i hagen.
Du har også fått en høyde max_height som beskriver hvor høyt gresset maksimalt skal være. Det betyr at hvis gresset er høyere enn denne høyden, skal det klippes ned til denne høyden.
I en fil clip_grass.py, lag en funksjon clip_grass som tar inn en liste av høyder heights og en høyde max_height. Funksjonen skal mutere listen heights slik at alle høyder som er større enn max_height blir klippet ned til max_height. Fordi funksjonen er destruktiv, trenger den ikke returnere noe.
I denne oppgaven har vi laget en urealistisk historie for å skape konteksten til oppgaven; men denne oppgaven er egentlig en nokså vanlig databehandlingsoppgave. Å «klippe» et signal betyr at vi endrer verdiene i en liste slik at de aldri overstiger en gitt terskel.
Dette gjøres for eksempel for å beskytte elektronikk fra å bli skadet av for høye signaler (dersom verdiene skulle bli benyttet for å styre et elektrisk spenningsnivå), eller motsatt; for å fjerne støy fra et målt signal.
Som et eksempel, hvis du har følgende liste med høyder:
[1, 2, 3, 4, 5]
Og maksimal høyde er 3, så vil listen etter klipping være:
[1, 2, 3, 3, 3]
Her er kode du kan lime inn på slutten av filen for å teste funksjonen din:
print("Testing clip_grass... ", end="")
# Case 1
heights = [1, 2, 3, 4, 5]
clip_grass(heights, 3)
assert [1, 2, 3, 3, 3] == heights
# Case 2
heights = [1, 2, 3, 3, 3]
clip_grass(heights, 3)
assert [1, 2, 3, 3, 3] == heights
# Case 3
heights = [10, 20, 200, 20, 400]
clip_grass(heights, 25)
assert [10, 20, 25, 20, 25] == heights
print("OK")
- For å mutere én enkelt posisjon i en liste
heights, bruk indeksering. For eksempel,- for å angi
5til indeks0kan du skriveheights[0] = 5, - for å angi
xtil indeksikan du skriveheights[i] = x.
- for å angi
-
Benytt en løkke som itererer over indeksene til listen
heights. Dette gjøres med en for-løkke som itererer overrange(len(heights)). Iteranden vil da få angitt en ny indeks for hver iterasjon av løkken.
Trylledrikker
Trollmannen Gallius har en liste over trylledrikker som han har brygget. Gallius har en liste over nivåer som beskriver hvor kraftige disse trylledrikkene er. Men Gallius har brygget så mange trylledrikker at han har mistet helt oversikten over hvor kraftige de forskjellige trylledrikkene er. Han trenger din hjelp til å normalisere nivåene slik at de ligger mellom 0 og 1.
Normalisering er en prosess som brukes for å endre verdier i en liste slik at de ligger innenfor et bestemt intervall, men samtidig beholder forholdstallet for forskjellene mellom verdiene. Det er for eksempel nokså vanlig er å normalisere verdier slik at de faller mellom 0 og 1, eller mellom -1 og 1 avhengig av data’ens natur.
Dette brukes for eksempel for lydspor hvor mikrofonen kan ha hatt ulik avstand til personen som prater i ulike opptak. Normaliseringen endrer volumet på lyden slik at de forskjellige lydsporene får omtrent samme volum likevel.
Det finnes ulike måter å normalisere data på, og den metoden vi beskriver i denne oppgaven er bare én metode.
For å normalisere nivåene til Gallius, må du finne den minste og største verdien i listen over nivåer (fremover referert til som henholdsvis low og high). Deretter må du gå gjennom listen og regne ut en ny verdi for hvert nivå. Den nye verdien skal være lik:
$$\frac{{level - low}}{{high - low}} $$
Det er disse nye verdiene som skal være resultatet av normaliseringen.
Som et eksempel, hvis Gallius har følgende liste over nivåer:
[1, 2, 3, 4, 5]
Da er minste verdi 1 og største verdi 5. For eksempel vil nivået 3 normaliseres til:
$$ \frac{{3 - 1}}{{5 - 1}} = \frac{2}{4} = 0.5 $$
Dette gir mening siden 3 er halvveis mellom 1 og 5 (som er minste og største verdi).
Som oppsummering:
I en fil normalize_potions.py, lag en ikke-destruktiv funksjon normalize_potions som tar inn en liste av nivåer levels og returnerer en ny liste med normaliserte nivåer. Hvis alle nivåene er like, skal funksjonen returnere en liste med samme lengde som levels hvor alle verdiene er 1. Hvis du ikke håndterer dette tilfellet, vil du få en ZeroDivisionError når du prøver å dele med high - low i formelen for normaliseringen. Du kan anta at levels alltid vil inneholde minst ett element.
Du kan kopiere følgende kode inn i normalize_potions.py for å teste funksjonen din:
print("Tester normalize_potions... ", end="")
# Første test
levels = [4, 3, 2, 1, 0]
expected = [1.0, 0.75, 0.5, 0.25, 0.0]
actual = normalize_potions(levels)
assert [4, 3, 2, 1, 0] == levels, "Funksjonen skal ikke mutere listen. Hvis du har brukt .sort() er listen mutert. Du kan bruke min og max for å finne minste og største verdi i listen uten mutasjon."
assert expected == actual, f"Forventet {expected} men fikk {actual}"
# Flere tester
assert [0.0, 0.25, 0.5, 0.75, 1.0] == normalize_potions([0.01,0.02,0.03,0.04,0.05])
assert [0.0, 0.25, 0.5, 0.75, 1.0] == normalize_potions([2, 3, 4, 5, 6])
assert [1.0, 1.0, 1.0, 1.0, 1.0] == normalize_potions([3, 3, 3, 3, 3])
assert [0.0, 0.3, 0.2, 0.9, 1.0] == normalize_potions([-1, 2, 1, 8, 9])
assert [1.0, 0.75, 0.5, 0.0] == normalize_potions([5, 4, 3, 1])
print("OK")
-
Husk!
minogmaxer innebygde funksjoner i Python som kan brukes til å finne henholdsvis minste og største verdi i en liste. -
Opprett en liste
normalizedsom skal inneholde de normaliserte verdiene. I begynnelsen kan den være en tom liste. -
Benytt en løkke som itererer over
levelsog regner ut den normaliserte verdien for hvert element. Legg den normaliserte verdien tilnormalized-listen. -
Husk å returnere!
Integraler
Denne oppgaven består av fire deler. Skriv alle funksjoner til de fire delene (A-D) i én felles fil, integrals.py.
Del A
I matematikken kan en funksjon for eksempel være definert som \(g(x) = \frac{1}{8}x^2 - 2x + 10\). La oss modellere denne matematiske funksjonen som en programmeringsfunksjon:
- I filen integrals.py, opprett en funksjon
gsom har en parameterxog som regner ut verdien av \(\frac{1}{8}x^2 - 2x + 10\) for den gitte verdien avx.
For eksempel skal et kall til g(8.0) returnere verdien 2.0, og et kall til g(4.0) skal returnere verdien 4.0.
Test koden din:
def almost_equals(a, b):
return abs(a - b) < 0.0000001
print("Tester g... ", end="")
# Første test
x = 8.0
actual = g(x)
expected = 2.0
assert almost_equals(expected, actual)
# Flere tester
assert almost_equals(4.0, g(4.0))
assert almost_equals(10.0, g(0.0))
print("OK")
Del B
I denne oppgaven skal vi regne ut en tilnærming for arealet under funksjonen \(g\) (fra del A) mellom to gitte punkter \(x_\text{lo}\) og \(x_\text{hi}\) på x-aksen. Vi antar at \(x_\text{lo} \leq x_\text{hi}\), og i denne omgang antar vi også at \(x_\text{lo}\) og \(x_\text{hi}\) er heltall.
For å gjøre vår tilnærming, skal vi enkelt nok regne ut summen av g(x_i) for alle heltalls-verdier \(x_i\) fra og med \(x_\text{lo}\) opp til (og ikke inkludert) \(x_\text{hi}\). For eksempel, dersom \(x_\text{lo} = 3\) og \(x_\text{hi} = 7\), er vi interessert i å vite hva summen \(g(3) + g(4) + g(5) + g(6)\) blir.
- I filen integrals.py, opprett en funksjon
approx_area_under_gmed parametrex_loogx_hisom returnerer summen avg(x_i)for alle heltallx_ifra og medx_loopp tilx_hi.

Test kode din:
print("Tester approx_area_under_g... ", end="")
# Første test
x_lo = 4
x_hi = 5
actual = approx_area_under_g(x_lo, x_hi)
expected = 4.0 # skal gi oss kun g(4), som altså er 4.0
assert almost_equals(expected, actual)
# Flere tester
assert almost_equals(3.125, approx_area_under_g(5, 6)) # g(5)
assert almost_equals(7.125, approx_area_under_g(4, 6)) # g(4)+g(5)
assert almost_equals(23.75, approx_area_under_g(1, 5)) # g(1)+g(2)+g(3)+g(4)
print("OK")
-
Opprett en variabel
running_totalsom i utgangspunktet er 0. Bruk denne variabelen som en løpende totalsum, for å holde styr på det totale arealet under grafen «så langt». -
Benytt en for-løkke som starter i
x_loog som går opp tilx_hi. Iteranden i løkken blir dax_i. For hver iterasjon av løkken, regn ut \(g(x_i)\) og legg dette til i den løpende totalsummen.
Del C
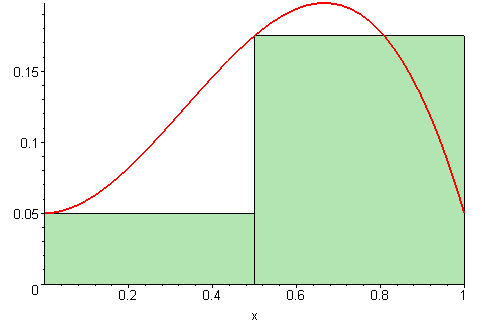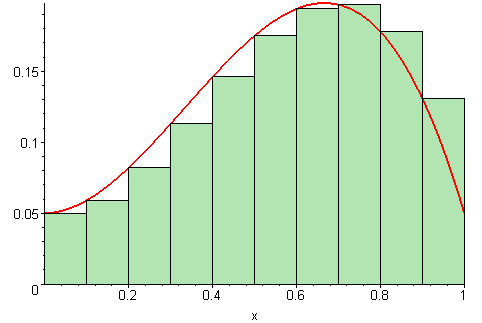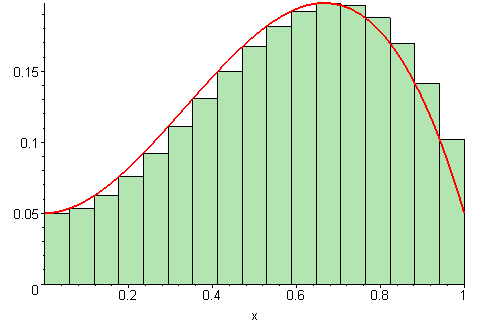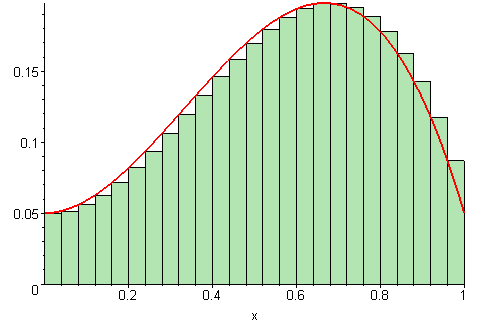
Estimatet for arealet vi regnet ut i forrige deloppgave er bare et estimat, siden vi later som funksjonen går i «trapper» i stedet for å være kontinuerlig, slik den egentlig er. For å gjøre estimatet vårt bedre, kan vi redusere bredden på hvert trappetrinn. Jo smalere trappetrinn vi velger, jo bedre blir estimatet vårt for arealet.
På figuren under vises det ulike bredder på trappetrinnene. Jo flere trappetrinn, jo mer nøyaktig vil arealet av det grønne området (som vi regner ut) stemme med det faktiske arealet under grafen (den røde streken).
Illustrasjon av 09glasgow09, CC BY-SA 3.0.
I denne oppgaven skal vi forbedre estimatet for arealet under grafen ved å la dem som kaller funksjonen vår bestemme hvor mange trappetrinn de ønsker å benytte. Dette kalles en (venstresidet) Riemann sum.1
-
I filen integrals.py, opprett en funksjon
riemann_sum_gmed parametrex_lo,x_hiogn. Funksjonen skal returnere en tilnærming av arealet under grafengfra oppgave A basert pånantall trappetrinn. -
På samme måte som i del B skal vi oppdatere en løpende total i en løkke.
-
På samme måte som i oppgaven «Oppdelt linjestykke» fra lab 3, skal vi dele opp linjestykket \([x_\text{lo}, x_\text{hi}]\) i \(n\) like store biter.
Merk: i denne oppgaven vet du allerede før løkken starter hvor mange iterasjoner løkken skal ha (nemlig
n). Derfor bør du velge enfor-løkke, og ikke en while-løkke. I denne oppgaven kan faktisk det å velge en while-løkke, i kombinasjon med avrundingsfeil som alltid vil skje når vi jobber med flyttall, gjøre at du får feil svar!
-
Legg merke til at hvert trappetrinn har bredde \(b = ({x_\text{hi} - x_\text{lo}})/{n}\).
-
Tenk på hvert trappetrinn som om det har et nummer \(i\). Som gode programmere bruker vi 0-indeksering – det vil si at vi tenker på det første trappetrinnet som nummer «0», det andre trappetrinnet er nummer «1», og så videre.
-
Observer at trappetrinn nummer \(i\) begynner på x-verdien \(x_i = x_\text{lo} + b \cdot i\). Det første trappetrinnet har nummer 0. Ergo begynner det første trappetrinnet ved \(x_\text{lo}\), det andre trappetrinnet begynner ved \(x_\text{lo} + b\), det tredje deretter begynner ved \(x_\text{lo} + 2b\) og så videre.
-
Bruk en løkke der iteranden er \(i\), altså nummeret til hvert trappetrinn. Da må løkken gå over heltallsverdier fra og med 0 opp til \(n\). Om du vet \(i\) kan du regne ut \(x_i\) som vist over.
-
For å regne ut arealbidraget fra trappetrinn \(i\), multipliser bredden \(b\) med høyden til trappetrinnet (husk: høyden til trappetrinnet er verdien \(g(x_i)\)).
Test koden din:
print("Tester riemann_sum_g... ", end="")
assert almost_equals(7.125, riemann_sum_g(4, 6, 2))
assert almost_equals(6.71875, riemann_sum_g(4, 6, 4))
assert almost_equals(6.3348335, riemann_sum_g(4, 6, 1000))
assert almost_equals(23.75, riemann_sum_g(1, 5, 4))
assert almost_equals(22.4375, riemann_sum_g(1, 5, 8))
assert almost_equals(21.166676666, riemann_sum_g(1, 5, 1_000_000))
print("OK")
Del D
Vi ønsker nå å regne ut arealet under flere grafer. Når alt kommer til alt er funksjonen \(g(x) = \frac{1}{8}x^2 - 2x + 10\) relativt obskur.
Opprett en funksjon riemann_sum med parametre f, x_lo, x_hi og n. Funksjonen skal returnere en tilnærming av arealet under grafen f mellom x_lo og x_hi basert på n antall trappetrinn. Koden vil være helt identisk med forrige deloppgave, bortsett fra at du kaller f(x_i) istedet for g(x_i) inne i løkken.
For å teste funksjonen, legg denne koden nederst i filen:
# Vi sjekker først at riemann_sum med funksjonen g som argument gir
# samme svar som riemann_sum_g -metoden fra forrige deloppgave.
print("Tester riemann_sum med funksjonen g... ", end="")
assert almost_equals(7.125, riemann_sum(g, 4, 6, 2))
assert almost_equals(6.71875, riemann_sum(g, 4, 6, 4))
assert almost_equals(6.3348335, riemann_sum(g, 4, 6, 1000))
assert almost_equals(23.75, riemann_sum(g, 1, 5, 4))
assert almost_equals(22.4375, riemann_sum(g, 1, 5, 8))
assert almost_equals(21.166676666, riemann_sum(g, 1, 5, 1_000_000))
print("OK")
# Så tester vi med et par andre funksjoner
# Funksjonen som kvadrerer, square(x) = x**2
def square(x):
return x**2
## Arealet under grafen square(x) = x**2 mellom 1 og 3
## Eksakt svar er 8 + 2/3, altså 8.66666666....
## Merk at vi kommer gradvis nærmere eksakt svar ved å øke n
print("Tester riemann_sum med funksjonen square... ", end="")
assert almost_equals(5.0, riemann_sum(square, 1, 3, 2))
assert almost_equals(7.88, riemann_sum(square, 1, 3, 10))
assert almost_equals(8.5868, riemann_sum(square, 1, 3, 100))
print("OK")
# Funksjonen som er en jevnt stigende, linear(x) = x
def linear(x):
return x
## Arealet under grafen for funksjonen f(x) = x mellom 2 og 4
## Eksakt svar er 6.
## Merk at vi kommer gradvis nærmere riktig svar ved å øke n
print("Tester riemann_sum med funksjonen linear... ", end="")
assert almost_equals(5.0, riemann_sum(linear, 2, 4, 2))
assert almost_equals(5.5, riemann_sum(linear, 2, 4, 4))
assert almost_equals(5.998046875, riemann_sum(linear, 2, 4, 1024))
print("OK")
-
Spesielt interesserte kan lese mer om ulike varianter av Riemann sum på Wikipedia. ↩︎
Flerfarget flagg
I filen multicolored_flag.py opprett en funksjon draw_multicolored_flagsom tar inn seks parametere: canvas, x1, y1, x2, y2, colors. Parameteren colors skal være en liste med strenger som representerer farger. Funksjonen skal tegne et flagg med vertikale striper på canvas med øvre venstre hjørne i punktet \((x_1, y_1)\) og nedre høyre hjørne i punktet \((x_2, y_2)\). Flagget skal ha like mange striper som det er farger i listen colors og hver oppføring i liste skal reflektere fargen på hver tilsvarende stripe. Første stripe skal altså ha farge colors[0], andre stripe skal ha farge colors[1], osv. Funksjonen trenger ikke å ha noen returverdi.
Merk: I filen multicolored_flag.py skal du ikke importere noe, og du skal heller ikke kalle på display-funksjonen. For å teste koden, opprett i stedet en separat fil multicolored_flag_test.py i samme mappe som multicolored_flag.py og kopier inn koden under. Når du kjører multicolored_flag_test.py, skal det tegnes tre flagg på skjermen som vist under:
from uib_inf100_graphics.simple import canvas, display
from multicolored_flag import draw_multicolored_flag
draw_multicolored_flag(canvas, 125, 135, 275, 265, ["red", "orange", "yellow", "green", "blue", "purple"])
draw_multicolored_flag(canvas, 10, 10, 40, 36, ["black", "yellow", "red"])
draw_multicolored_flag(canvas, 10, 340, 390, 360, ["black", "white", "black","black", "white", "black","black", "white", "black"])
display(canvas)

PS: Når du kaller på canvas.create_rectangle, legg til
outline=""i argumentlisten. Da unngår du at det tegnes en svart ramme rundt rektangelet.
PPS: Om du syntes denne oppgaven var mistenkelig lik siste del av forrige ukes tog-oppgave, har du helt rett. Forskjellen er at den er obligatorisk denne uken. Du kan bruke din egen kode om igjen hvis du vil (yes! endelig får du sjansen til å sitere deg selv!).
Farget rutenett
I filen colored_grid.py opprett en funksjon draw_grid som tar in følgende parametre: canvas, x1, y1, x2, y2, color_grid. Parameteren color_grid er en 2D-liste med strenger som representerer farger.
Funksjonen skal tegne et rutenett med farger med øvre venstre hjørne i punktet \((x_1, y_1)\) og nedre høyre hjørne i punktet \((x_2, y_2)\). Fargene i listen color_grid skal reflektere fargen på rutene i tilsvarende posisjon (se eksempelkjøringen). Funksjonen trenger ikke å ha noen returverdi.
Merk: I filen colored_grid.py skal du ikke importere noe, og du skal heller ikke kalle på display-funksjonen. For å teste koden, opprett i stedet en separat fil colored_grid_test.py i samme mappe som colored_grid.py og kopier inn koden under. Når du kjører colored_grid_test.py, skal det tegnes tre rutenett på skjermen som vist under:
from uib_inf100_graphics.simple import canvas, display
from colored_grid import draw_grid
# Et 4x2 rutenett med farger
draw_grid(canvas, 40, 100, 120, 180, [
["red", "darkred"],
["yellow", "orange"],
["white", ""],
["cyan", "blue"],
])
# Et sjakkbrett
draw_grid(canvas, 170, 30, 370, 250, [
["white", "black"] * 4,
["black", "white"] * 4,
] * 4)
# En 2D-liste med kun én rad
draw_grid(canvas, 50, 310, 350, 370, [
['#00c', '#01c', '#02c', '#03c', '#04c', '#05c', '#06c', '#07c',
'#08c', '#09c', '#0ac', '#0bc', '#0cc', '#0dc', '#0ec', '#0fc']
])
display(canvas)
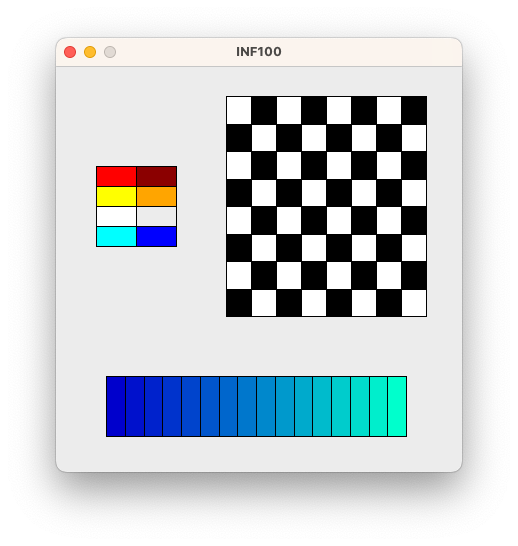
PS: I denne oppgaven skal outline være med når du tegner rektangler.
-
Begynn med å definere to variabler
rowsogcolssom representere antall rader og antall kolonner i rutenettet. Antall rader er lengden på den ytre listen (len(color_grid)) mens antall kolonner er lengden på den første indre listen (len(color_grid[0])). Vi antar at det er like mange kolonner i hver rad, slik at vi ikke trenger å sjekke alle. -
Definer to variabler
cell_widthogcell_heightsom representerer henholdsvis bredden og høyden på en celle i rutenettet. Bredden til en celle vil være differansen mellom x-koordinatene delt på antall kolonner, mens høyden til en celle vil være differansen mellom y-koordinatene delt på antall rader. -
La oss gå gjennom hver eneste mulige kombinasjon av en rad og en kolonne. La
rowogcolvære iterandene i to nøstede for-løkker; larowgå fra 0 opp til (ikke inkludert)rows, og lacolgå fra 0 og opp til (men ikke inkludert)cols. -
Inne i den nøstede løkken skal vi tegne cellen i rad
rowog kolonnecol. For å tegne cellen, må vi regne ut koordinatene(cell_x1, cell_y1)som er punktet til venstre øverst i cellen, og punktet(cell_x2, cell_y2)som er punktet til høyre nederst.- For å regne ut
cell_x1, begynner vi på koordinatetx1og flytter osscell_widthpiksler til høyrecolganger. - For å regne ut
cell_y1, begynner vi på koordinatety1og flytter osscell_heightpiksler nedoverrowganger. - For å regne ut
cell_x2, begynn påcell_x1og flytt degcell_widthpiksler til høyre. - For å regne ut
cell_y2, begynn påcell_y1og flytt degcell_heightpiksler nedover.
- For å regne ut
-
Etter at du har regnet ut koordinatene til cellen, kall
create_rectanglepåcanvas. Etter de posisjonelle argumentene vi regnet ut over, brukfill=color_grid[row][col]for å sette fargen.
Valgfri
Alternerende sum
I filen alternating_sum.py opprett funksjonen alternate_sign_sum som tar inn en liste med tall summands som parameter. Funksjonen skal regne ut den alternerende summen av tallenen i listen summands (summands[0] - summands[1] + summands[2] - summands[3] … summands[n-1]).
Test koden din ved å legge til disse linjene nederst i filen:
print("Tester alternate_sign_sum... ", end="")
assert(3 == alternate_sign_sum([1, 2, 3, 4, 5]))
assert(30 == alternate_sign_sum([10, 20, 30, 40, 50]))
a = [-10, 20, -30, 40, -50]
assert(-150 == alternate_sign_sum([-10, 20, -30, 40, -50]))
assert([-10, 20, -30, 40, -50] == a) # Sjekker at funksjonen ikke er destruktiv
print("OK")
-
Vi trenger å bruke en løkke for å gå igjennom alle elementene i listen. Siden vi vet allerede før løkken begynner hvor mange iterarsjoner vi skal ha (nemlig
len(summands)), bør vi bruke en for-løkke -
Før løkken starter, opprett en variabel som holder den løpende totalsummen. For hver iterasjon av løkken legger vi til (eller trekker fra) et tall til denne variabelen.
-
Inne i løkken må vi avgjøre om vi skal legge til eller trekke fra i den iterasjonen som nå skal utføres. Hvis vi benytter en indeksert løkke, kan vi sjekke om indeks er et partall eller oddetall, og slik velge om vi legger til eller trekker fra.
-
Returner totalsummen når løkken er ferdig.
Minste absolutt-forskjell
I filen least_difference.py skriv funksjonen smallest_absolute_difference som har en liste med tall a som parameter. Funksjonen skal returnerer den minste absolutt-verdi som er forskjellen mellom to tall i listen a.
Test koden din ved å legge til disse linjene nederst i filen:
print("Tester smallest_absolute_difference... ", end="")
assert(1 == smallest_absolute_difference([1, 20, 4, 19, -5, 99])) # 20-19
assert(6 == smallest_absolute_difference([67, 19, 40, -5, 1])) # 1-(-5)
assert(0 == smallest_absolute_difference([2, 1, 4, 1, 5, 6])) #1-1
a = [50, 40, 70, 33]
assert(7 == smallest_absolute_difference(a))
assert([50, 40, 70, 33] == a) # Sjekker at funksjonen ikke er destruktiv
print("OK")
Alternativ A (kanskje enklest å komme på, men litt ineffektivt):
- Før løkkene starter, opprett en variabel som har til hensikt å hold på den minste forskjellen mellom to elementer sammenlignet så langt. Initielt kan den for eksempel ha absolutt-verdien av avstanden mellom de to første elementene i listen
- Benytt en indeksert for-løkke for å gå igjennom alle elementene i listen. I iterasjon nummer
iav løkken er hensikten å finne den minste absolutt-verdi-forskjellen mellom elementeta[i]og et element som kommer senere i listen (vi trenger kun å sjekke det som kommer senere i listen – fordi hvis den minste forskjellen var mot et element tidligere i listen, vil denne forskjellen allerede være funnet da vi sjekket det elementet). - Benytt en nøstet for-løkke for å gå gjennom alle posisjoner
jmellomi+1oglen(a); regn ut absolutt-verdien av forskjellen påa[i]oga[j], og dersom den er mindre enn noe vi har sett før, lagre denne avstanden i variabelen som har til hensikt å huske dette. - Når alle iterasjonene er ferdig, returner svaret
Alternativ B (mer effektivt):
-
Ikke-destruktivt sorter listen
-
Gå gjennom listen med en indeksert løkke, og regn ut forskjellen på alle etterfølgende elementer. Ta vare på den minste slike avstanden.
Ordspill
Denne oppgaven består av to deler. Skriv funksjoner til begge deloppgaver (A-B) i én felles fil, word_games.py.
I denne oppgaven skal vi skrive et hjelpemiddel for deg som ønsker å bli bedre i ordspill som Scrabble og Wordfeud. Det er selvfølgelig ikke lov å bruke dette for å jukse når man spiller, men det er lov å bruke det for å evaluere spill i etterkant.
I spill som Scrabble og Wordfeud har hver spiller en bunke med brikker, som hver har én bokstav på seg. Poenget er å kombinere brikkene slik at de former et lovlig ord.
Del A
Opprett en funksjon can_be_made_of_letters(word, letters) som tar inn en streng word og en streng letters som parametre. Funksjonen skal returere True hvis strengen word kan lages med bokstavesamlingen letters, og False hvis ikke.
Test koden din ved å legge til disse linjene nederst i filen:
print("Tester can_be_made_of_letters... ", end="")
assert(can_be_made_of_letters("emoji", "abcdefghijklmno"))
assert(not can_be_made_of_letters("smilefjes", "abcdefghijklmnopqrs"))
assert(can_be_made_of_letters("smilefjes", "abcdeeefghijklmnopqrsss"))
assert(can_be_made_of_letters("lese", "esel"))
# Ekstra tester for mer avansert variant, med wildcard * i bokstavene
# assert(can_be_made_of_letters("lese", "ese*"))
# assert(not can_be_made_of_letters("lese", "esxz*"))
# assert(can_be_made_of_letters("smilefjes", "s*i*e*j*s"))
# assert(not can_be_made_of_letters("smilefjes", "s*i*e*j*z"))
print("OK")
Sjekk for hver bokstav i ordet som skal lages om antall forekomster av bokstaven i bokstavsamlingen er tilstrekkelig i forhold til antall forekomster av bokstaven i ordet. Strenger har en metode .count som kan brukes til dette.
Del B
Opprett en funksjon possible_words(wordlist, letters) som tar inn en liste med strenger wordlist og en streng letters som parametre. Funksjonen skal retunere en liste med alle ord fra wordlist som kan lages med bokstavene i letters.
Test koden din ved å legge til disse linjene nederst i filen:
print("Tester possible_words... ", end="")
hundsk =["tur", "mat", "kos", "hent", "sitt", "dekk", "voff"]
kattsk =["kos", "mat", "pus", "mus", "purr", "mjau", "hiss"]
assert(['kos', 'sitt'] == possible_words(hundsk, "fikmopsttuv"))
assert(['kos', 'pus', 'mus'] == possible_words(kattsk, "fikmopsttuv"))
# Ekstra tester for mer avansert variant, med wildcard * i bokstavene
# assert(['tur', 'mat', 'kos', 'sitt'] == possible_words(hundsk, "fikmopsttu*"))
# assert(['kos', 'mat', 'pus', 'mus'] == possible_words(kattsk, "fikmopsttu*"))
print("OK")
Komprimering
Denne oppgaven består av to deler. Skriv funksjoner til begge deloppgaver (A-B) i én felles fil, runlength_encoding.py.
En fil består av en sekvens av 1’ere og 0’ere. Noen filformater har i praksis veldig lange sekvenser med kun 1’ere eller kun 0’ere. For eksempel: en sensor i et alarmsystem gir 1 som output når en dør er åpen, og 0 som output når en dør er lukket; sensoren blir avlest 1 gang i sekundet, og disse data’ene blir lagret som en sekvens av 0’ere og 1’ere i en fil. Et annet eksempel på slike filer er bilder med store hvite eller svarte felter.
For å komprimere slike filer, kan vi omgjøre måten vi skriver filen på til å bestå av en sekvens heltall som forteller vekselvis hvor mange 0’ere og 1’ere som kommer etter hverandre. Det første tallet i komprimeringen forteller hvor mange 0’er det er i begynnelsen. Dette tallet kan være 0 dersom binærtallet begynner med 1. Alle andre tall i komprimeringen vil være positive. Du kan lese mer om denne typen komprimering på Wikipedia.
For enkelhets skyld gjør vi denne oppgaven med strenger og lister og ikke direkte med 1’ere og 0’ere lagret i minnet.
Del A
Opprett en funksjon compress(raw_binary) som tar inn en streng raw_binary bestående av 0’ere og 1’ere. Funksjonen skal retunerer en liste som representerer sekvensen i komprimert form (tall skilles med mellomrom).
Test koden din ved å legge til disse linjene nederst i filen:
print("Tester compress... ", end="")
assert([2, 3, 4, 4] == compress("0011100001111"))
assert([0, 2, 1, 8, 1] == compress("110111111110"))
assert([4] == compress("0000"))
print("OK")
-
Det finnes mange måter å løse dette problemet på. Det kan være lurt å begynne med å sjekke om første tegn er “1”. Hvis det er tilfelle legg til 0. Fordi 0 indikerer at det første tegnet ikke er «0».
-
Lag en variabel som begynner på 0 (int) den kan brukes for å telle antall 0’ere og 1’ere, og en tom liste.
-
Lag en løkke som går fra 0 opp til lengden av stringen - 1. Dette lar oss sammenligne to tegn samtidig.
-
I løkken sjekk om tegnet er lik neste tegn, feks “if [i] == [i + 1]:” hvis dette er True øk telleren med 1. Hvis dette ikke stemmer legg verdien til telleren i listen, og tilbakestill teleren til 1.
-
Når løkken er feridg legg till telleren i listen igjen.
-
Bruk join funksjonen til å konvertere listen til en string, return den stringen.
-
Pass på å bruke str() for å konvertere int til str.
Del B
Opprett en funksjon decompress(compressed_binary) som tar inn en liste compressed_binary beståenden av heltall som representerer en komprimert sekvens av 0’ere og 1’ere. La funksjonen returnere den ukomprimerte sekvensen av 0’ere og 1’ere.
Test koden din ved å legge til disse linjene nederst i filen:
print("Tester decompress... ", end="")
assert("0011100001111" == decompress([2, 3, 4, 4]))
assert("110111111110" == decompress([0, 2, 1, 8, 1]))
assert("0000" == decompress([4]))
print("OK")